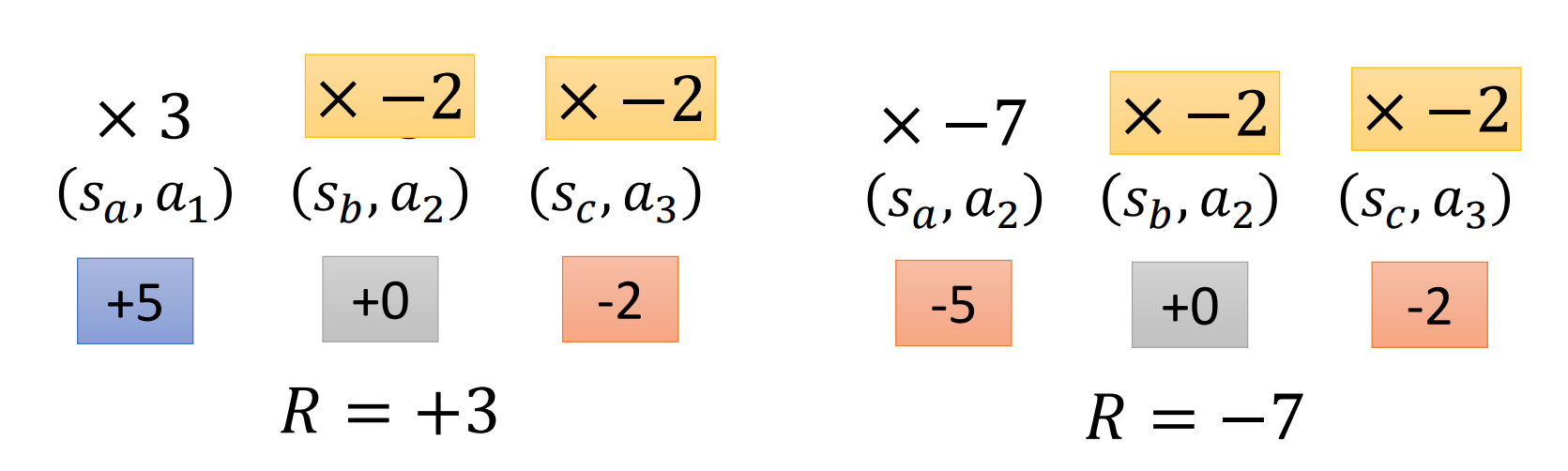Deep Reinforcement Learning
Notes on DRL Course By Hung-yi Lee
深度强化学习
Policy Gradient
算法主要包括三个主要部分:Actor、Environment、Reward
Environment和Reward在初始时给定,而Actor则在与环境的交互中学习Policy
其一轮的交互过程称为
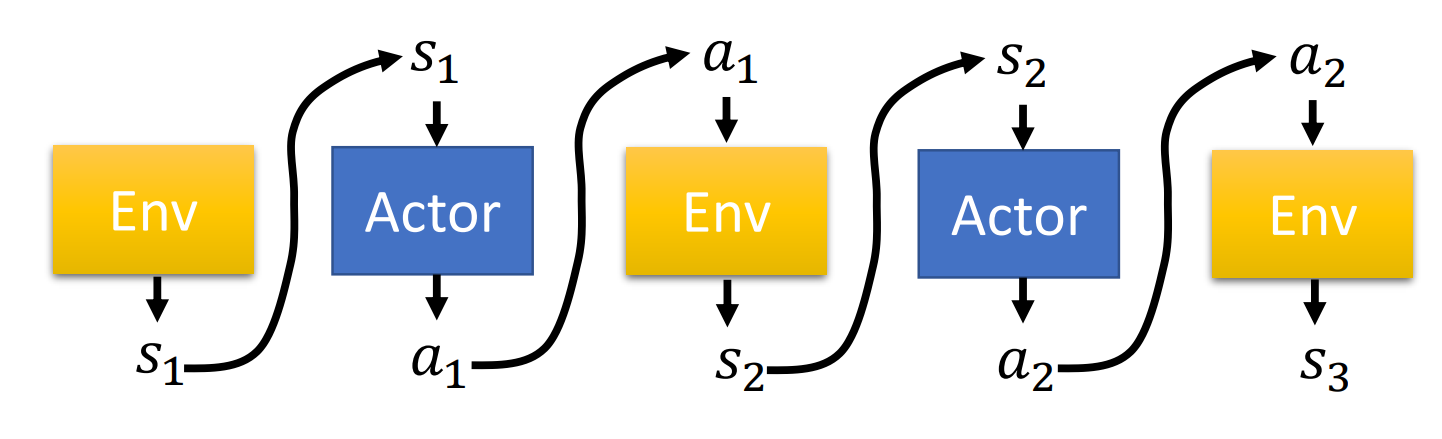
Trajectory,如下图所示,形式化表述为$Trajectory \ \tau = {s1,a_1,s_2, a_2,\cdots,s_T,a_T}$$Trajectory \ \tau$可以使用概率分布来描述,过程中的每一步都是概率性的
比如Environment在某一状态$s_1$接收到Actor的某一动作$a_1$输入时,其转变到另一个状态$s_2$可以用条件概率$p(s_2 s_1,a_1)$表示;Actor在接收的输入的某一状态$s_1$输入时,执行动作$a_1$的概率可以表示为$p_\theta(a_1 s_1)$,其中$\theta$为Actor的Policy Network的模型参数 某Trajectory $\tau$的概率则可以使用下述式子表示,即一个随机过程的概率 \(\begin{aligned} p_\theta(\tau) &=p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)p_\theta(a_2|s_2)p(s_3|s_2,a_2)\cdots\\ &= p(s_1)\prod_{t=1}^T p_\theta(a_t | s_t)p(s_{t + 1} | s_t, a_t) \end{aligned}\)
Actor在对Environment执行动作后,可以获得一个奖励反馈$r_t$,在整个$Trajectory$中所有的奖励反馈之和即为该$Trajectory$的奖励,即$R(\tau) = \sum_{i=1}^T r_t$
那么期望的奖励可以表示为$\overline{R_\theta}=\sum\limits_\tau R(\tau)p_\theta(\tau)=E_{\tau\sim p_\theta(\tau)}[R(\tau)]$
Policy Gradient的目的就是最大化期望的奖励,通过求解$\overline{R_\theta}$的梯度来更新Policy的参数$\theta$ \(\begin{aligned} \nabla \overline{R}_\theta &= \sum_\tau R(\tau)\nabla p_\theta(\tau)\\ &= \sum_\tau R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}\\ &= \sum_\tau R(\tau) p_\theta(\tau) \nabla \log{p_\theta(\tau)}\\ &= E_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log{p_\theta(\tau)}]\\ &\approx \frac{1}{N}\sum_{n=1}^N R(\tau^n)\nabla\log p_\theta(\tau^n) \left( \text{通过蒙特卡洛方法进行采样求均值}\right)\\ &= \frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}R(\tau^n_t)\nabla\log{p_\theta^n(a^n_t | s^n_t)}\left(\text{通过将}p_\theta(\tau)\text{的计算公式代入,环境的状态转变概率为常数,故省去}\right) \end{aligned}\)
由上述方法计算出期望奖励$\overline{R_\theta}$关于Policy参数$\theta$的梯度,由此更新参数$\theta \leftarrow \theta + \eta \nabla\overline{R}_\theta $
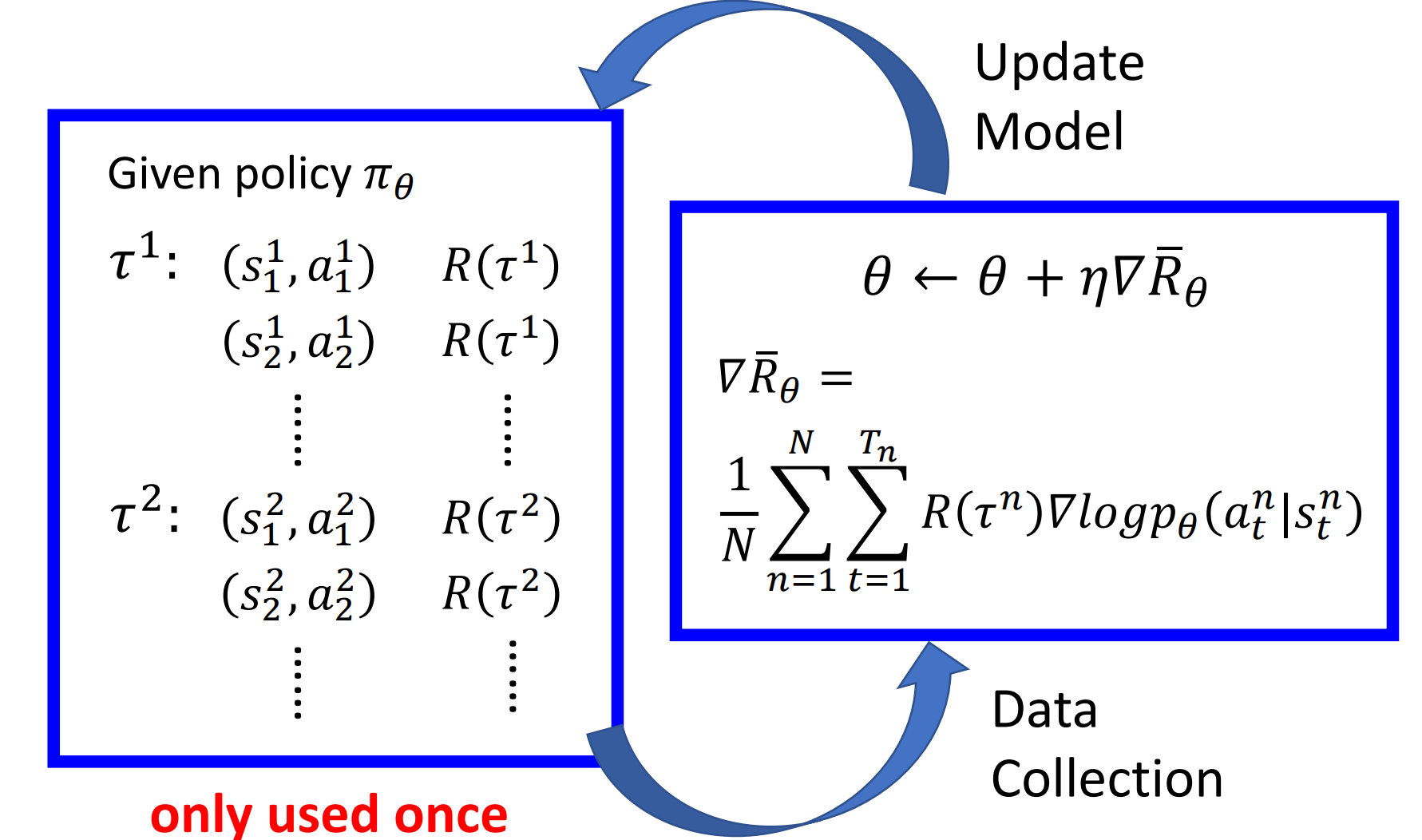
具体过程如下图所示,Actor通过与环境交互收集数据$\tau_1\sim\tau_N$,然后通过计算梯度来更新参数$\theta$,数据只会被使用一次,然后通过更新参数的Actor采集新的数据,如此往复
其本质上就是在促使Policy增加那些能够带来较大收益的动作的概率,并减小那些带来负收益的动作的概率
实现细节
添加baseline
在有些情景下,收益(Reward)的值可能是非负的值,因此梯度更新时,所有采样的动作的概率都会得到提升,只是提升的程度不同
但是如果某个动作在某轮数据采集中没有被采样到,但是实际上该动作相较其他被采样的动作能带来更大的收益,在更新Policy参数时,由于其他动作的概率提升了,因此该更优的动作的执行概率就相对降低
这种情况是我们不希望出现的,因此可以将奖励函数减去人为设定的baseline值,来避免此问题 \(\nabla\overline{R}_\theta\approx\frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}(R(\tau^n_t)-b)\nabla\log{p_\theta^n(a^n_t | s^n_t)}\)
给每个动作设置合适的分数
在当前所推导的梯度计算公式中,同一trajectory的动作的奖励都是一样的,即$R(\tau^n_t)-b$
但其实同一trajectory中不同阶段所执行的动作对最终的奖励贡献是不一样的
为了区分这一点,引入了优势函数(Advantage Function)这一概念
其思想是,当前的动作只会影响到后续的一系列动作,而不会影响前面已经发生过的<State, Action> pair,那么就可以求出针对每个(s,a)的奖励函数,$R(\tau)=\sum_{t^{\prime}=t}^{T_n} r_{t^\prime}^n$
再引入一个衰减系数(discount factor),来弱化对距离当前(s,a)较远的行为的贡献,最后针对每个(s,a)奖励函数计算公式如下 \(\sum_{t^\prime=t}^{T_n}\gamma^{t^\prime-t}r_{t^\prime}^n\)
On-Policy $\rightarrow$ Off-Policy
On-Policy:与环境交互的agent和要学习的agent是同一个Off-Policy:与环境交互的agent和要学习的agent不是同一个